There is an enormous research effort currently going on around two major machine learning buzz words: graph embeddings and neural architecture search. Their core problems are highly related and fooling around with thoughts about connections to biology leads me to a statement I currently find quite fascinating: our brain could entirely encode different computational structures, flood parts of its underlying hardware in the face of a situation with one encoded structure and then run inferences over that structure with a situational representation. Sounds complex, but a direct implication of that would be that even if we would understand the biological neural wiring of various brains we could not simply deduce information from one brains' activity by understanding the brain activity of another one with an equivalent wiring.
Graph embeddings can be understood as continuous representations of discrete objects or as an example something like a real number $(0.3, -11.193, 17)^T = a\in\mathbb{R}^3$ associated to a graph $\circ \rightarrow \circ \rightarrow \circ$ – of which we know that they don’t have canonical representations. Usually graphs are written down formally with all their vertices $V$ and edges $E \subset V\times V$ and adjacency matrix or adjacency list are common representations. However, two adjacency matrices can refer to the structurally equivalent graph – a circumstance usually referred to as the graph isomorphism problem of which theoretical computer science currently does not even know whether its just in the complexity class $P$ or even strictly in $NP$. Finding good graph embeddings in context of a more complex optimization target includes typically to have two close embeddings $h_1$ and $h_2$ for structurally similar graphs $g_1$ and $g_2$ and another distant embedding $h_3$ for a structurally dissimilar graph $g_3$. Such continuous vectors would enable some arithmetic capabilities as in word embeddings and one could – based on the nature of the particular embedding – calculate distances (= metrics) between them: $|h_1-h_2| < |h_2-h_3|$. In context of a particular optimization target this also means that the obtained embeddings and metrics used over those embeddings can be approximations to the graph isomorphism problem – knowing whether $g_1$ is structurally equivalent or close to $g_2$ while $g_3$ is not.
Neural Architecture Search on the other hand can be understood as a subfield to automated machine learning and seeks to investigate methods to find optimal architectures of deep learning models in context of a given problem domain or in a universal manner. As the engineering aspect got more and more complex over the last years I found the term computational graphs to be quite useful as to refer to graphs with vertices of any kind of computation while neural networks are more fundamentally having neurons and are thus more constrained. Computational graphs are thus more decoupled of the original concept of neural networks consisting of non-linear activations of weighted aggregated inputs. This makes them more powerful but at the same time makes the understanding of their graphs way more difficult. As it can be easily seen, graphs play an important role when looking at automated ways to find optimal graphs for neural networks or general computational graphs.
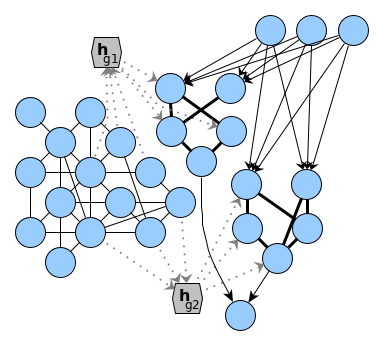
Let me get back to the initial statement that brains could encode different computational structures: well, obviously in an approximate way that is possible because it simply requires any kind of encoding a graph. But whether the brain could flood parts of its underlying hardware with one encoded structure is an entire different statement. Such flooding requires the capability to decode a continuous graph embedding into an abstraction layer (like the actual biological neurons) on which computations could be inferred on. In the attached figure I sketched a network, e.g. of a recurrent neural network function or a reservoir model and two graph embeddings $h_{g1}$ and $h_{g2}$ which are contained in the representation of the model. I am unsure about how the transformational step from these representations into the right part of the sketch could take place – a flodding of parts of the network with a structure decoded from a graph embedding.
Having a generative model of graphs with an appropriate flexibility on e.g. the number of vertices is usually auto-regressive and thus quite complex. Such a model requires some information of time, either in form of observed data from outside the model or within the model e.g. as a recurrent model, making it a complex dynamical system. The other part, however, could be simply directed and acyclic as a lot dynamical information could be stored already in various kinds of structures. This idea leads me to imagining a brain which could be partially complex and recurrent while another part could be directed and computationally very fast. Ultimately, those questions and thoughts lead me to read more on neuroscientific results on what is known about the actual workings in brain dynamics. As to my best knowledge, it is still unknown why neurons change and whether there are more levels of information processing than the signal processing through dendrites and neurons. Also, backpropagation in a deeper sense seems to be very unlikely. But I could imagine that the structure could have an influence on local learning principles which might be based on information from differences similar to gradients and backprop.
References
@article{kingma2013auto,
title={Auto-encoding variational bayes},
author={Kingma, Diederik P and Welling, Max},
journal={arXiv preprint arXiv:1312.6114},
year={2013}
}